[Paper Review] LoRA: Low-Rank Adaptation of Large Language Models
Introduction
Finetuning all model parameters of a large language model is prohibitively expensive. Existing works tried to mitigate costs by partially updating parameters or employing external modules that have relatively fewer parameters. However, these approaches led to inference latency or reducing sequence length and failed to solve a trade-off between cost-effectiveness and model performance. Thus, the authors introduce a novel method, called low-rank adaptation (LoRA).
Previous works [1, 2] showed that pre-trained over-parameterized models are actually a low-dimensional property. Inspired by these findings, they assumed the finetuning process also has a low intrinsic rank; The rank of a matrix is the dimension of the vector space. A key idea of Low-rank adaptation is to indirectly train rank decomposition matrices instead of directly updating model weights.
Problem Statement
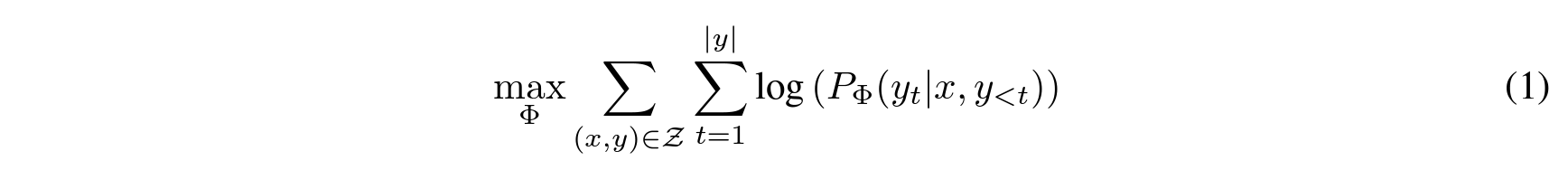
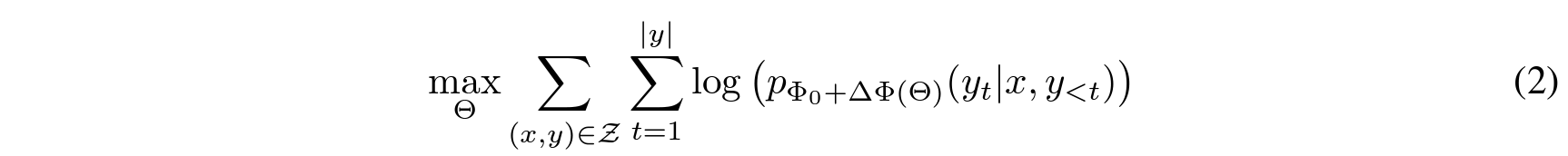
As shown in equations, equation (1) shows the the conditional language modeling objective in case of full finetuning, while equation (2) is the LoRA objective. Since the number of model parameters (Phi) is much greater than the number of LoRA paramters (Theta), a low-rank representation is cost-efficient. According to the paper, the number of LoRA parameters is only about 0.01% of that from GPT-3 175B.
Method
Low-rank Decomposition
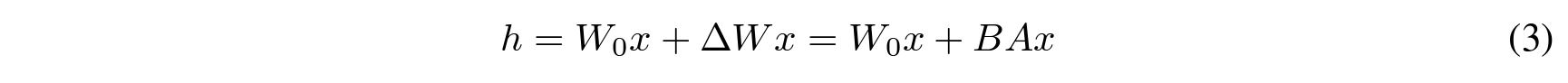
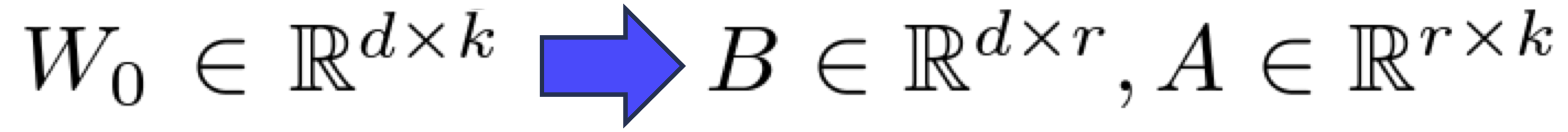
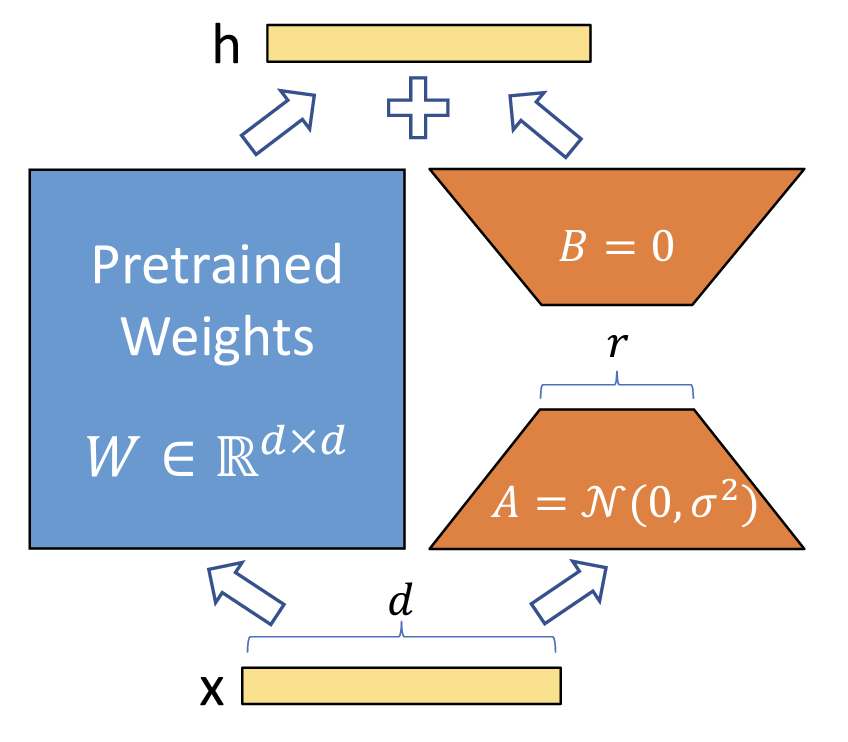
Let W0 (d x k) denote a pre-trained model weight. The authors re-parametrized ∆W into B x A, where the rank r « min(d, k). This low-rank decomposition scheme resulted in successful finetuning performances while ensuring cost-effectiveness without critical inference latency. In addition, by increasing the number of parameters (rank r), LoRA also converges to the case of full finetuning the original model.
Applying LoRA to Transformer
Revisiting the transformer architecture, there are four parameters in the self-attention module and two matrices in the MLP module. In this paper, they only treated query, key, and value for downstream tasks and freezed the MLP module for simplicity and memory efficiency.
Practical Benefits and Limitations
In perspective of memory and storage usage, LoRA achieved practical advantages. In the case of GPT-3 175B, they reduced VRAM up to 2/3 (from 1.2TB to 350GB) and 10,000 times smaller storage (from 350GB to 35MB).
LoRA also has its limitations that is not suitable for multi-task problems. By taking the risk of inherent inference latency, a potential solution lies in the implementation of dynamically loaded LoRa modules.
Experimental Results
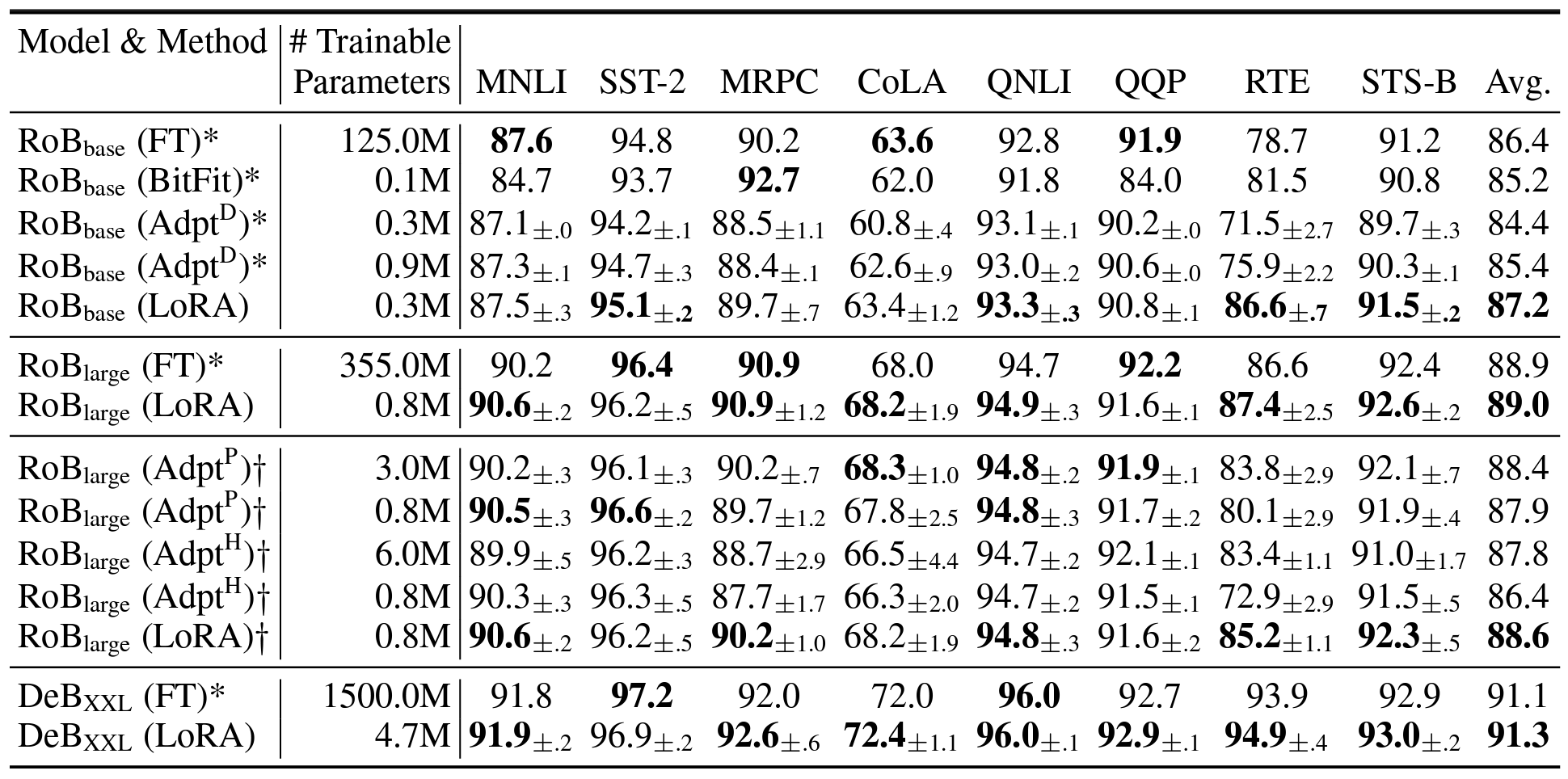
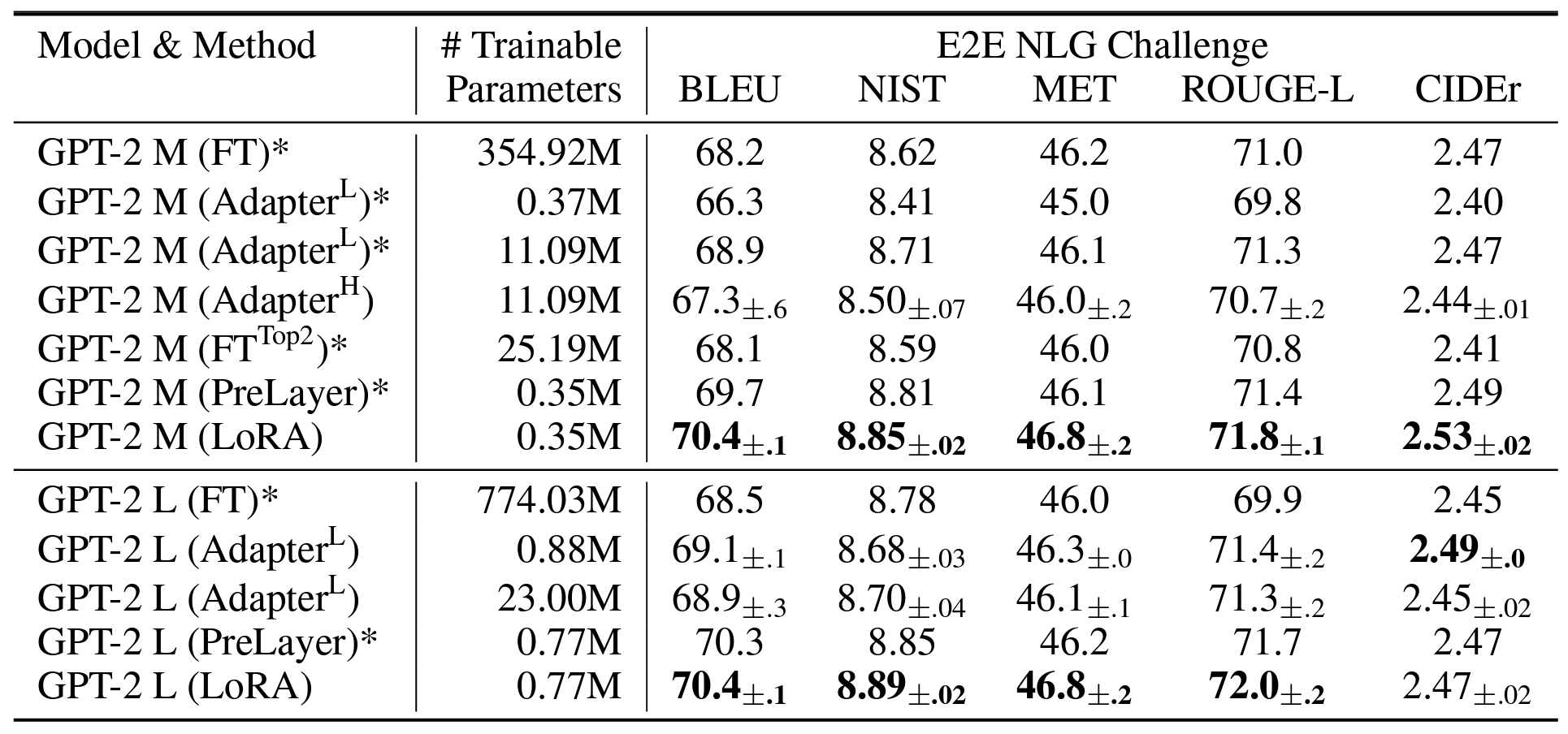
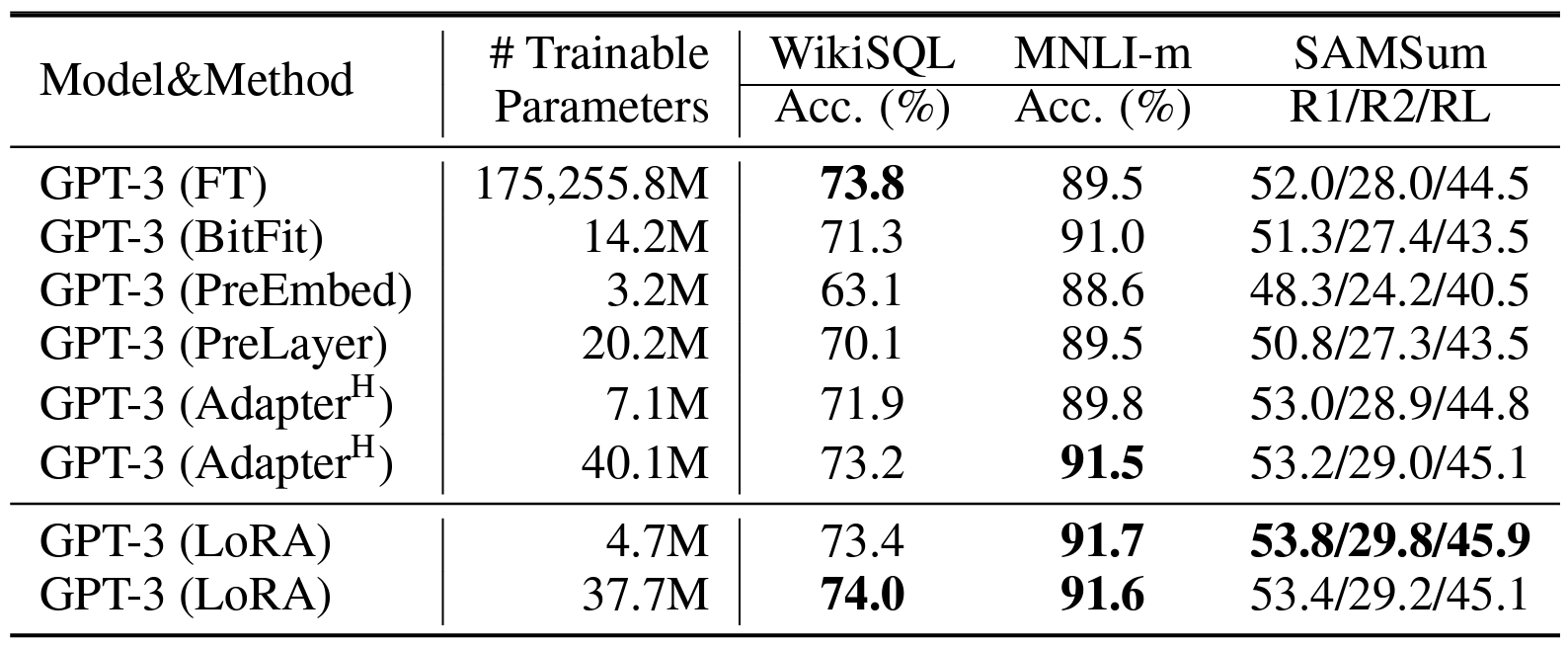
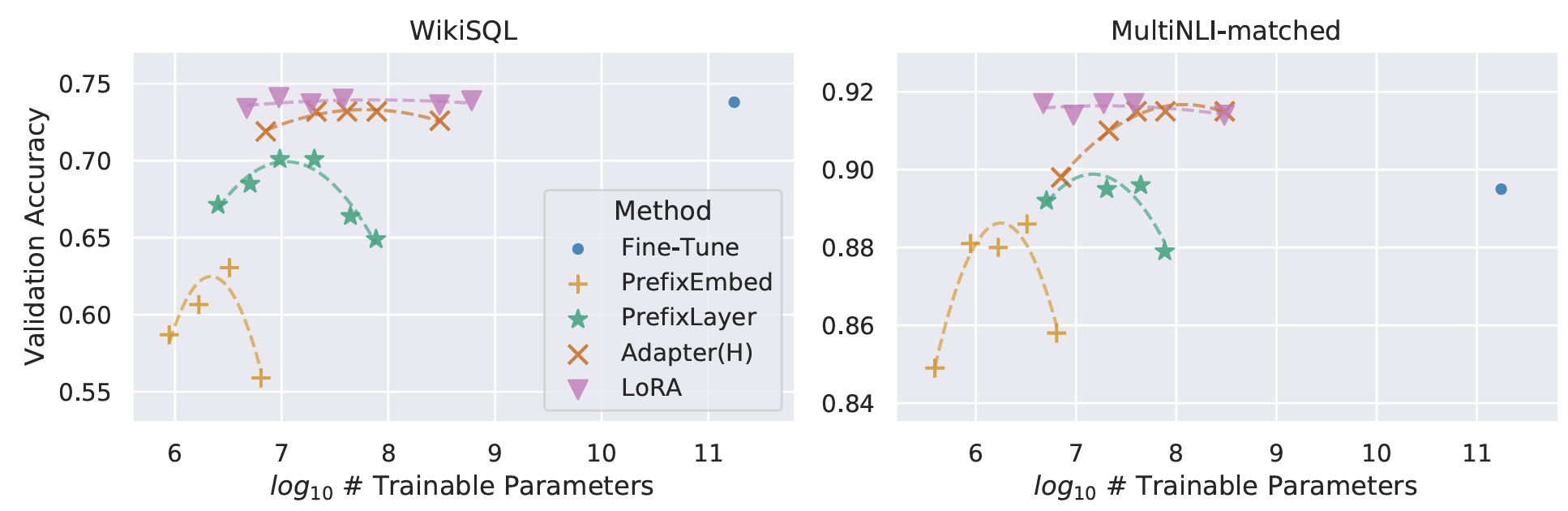
As shown in tables and the figure, LoRA achieved comparable or best performances compared to the prior works. Particularly, LoRA also exhibits better scalability and task performance among the benchmarks.
Conclusion
Remaining parts are about investigations of the hyperparameter rank r, attention matrices, and correlation between W and ∆W. It was surprising that employing a simple matrix decomposition scheme can improve performance and practical benefits.
References
[1] Li, Chunyuan, et al. “Measuring the intrinsic dimension of objective landscapes.” arXiv preprint arXiv:1804.08838 (2018).
[2] Aghajanyan, Armen, Luke Zettlemoyer, and Sonal Gupta. “Intrinsic dimensionality explains the effectiveness of language model fine-tuning.” arXiv preprint arXiv:2012.13255 (2020).
