[Paper Review] QLoRA: Efficient Finetuning of Quantized LLMs
Introduction
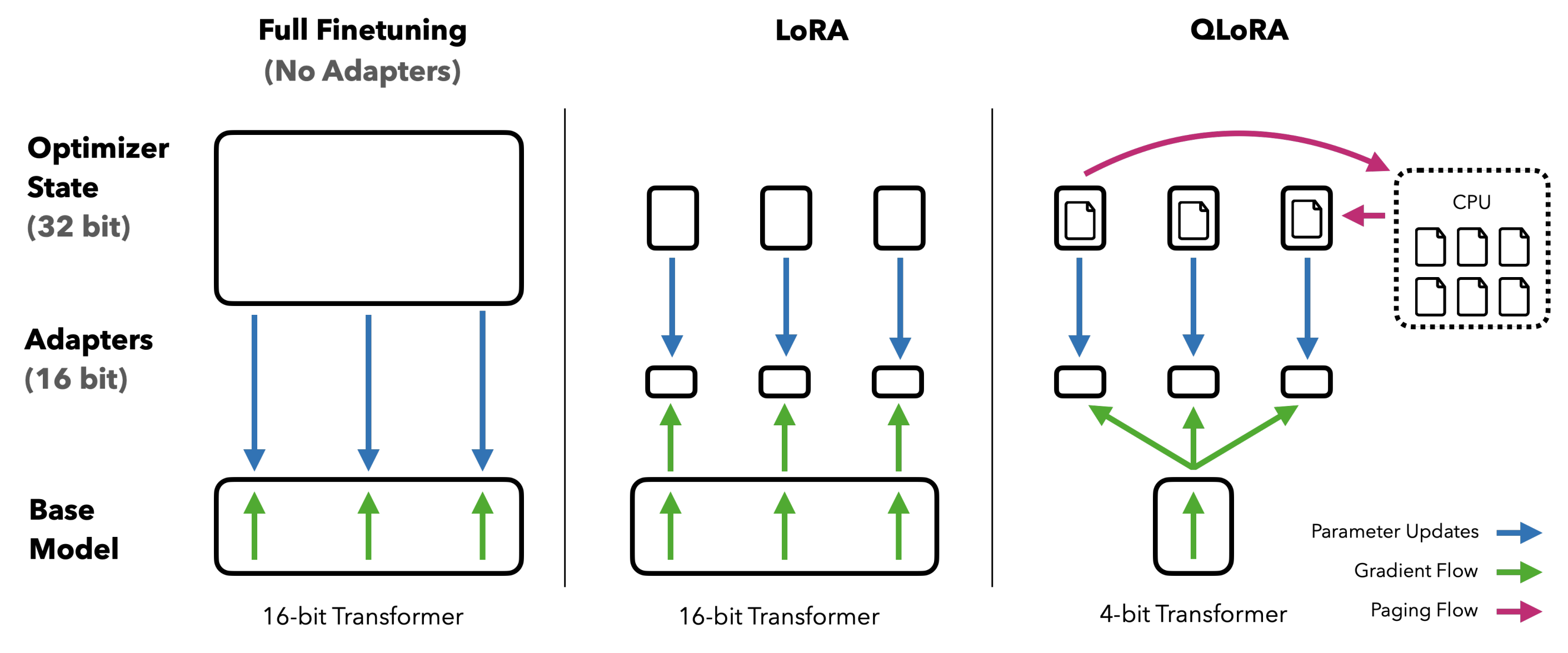
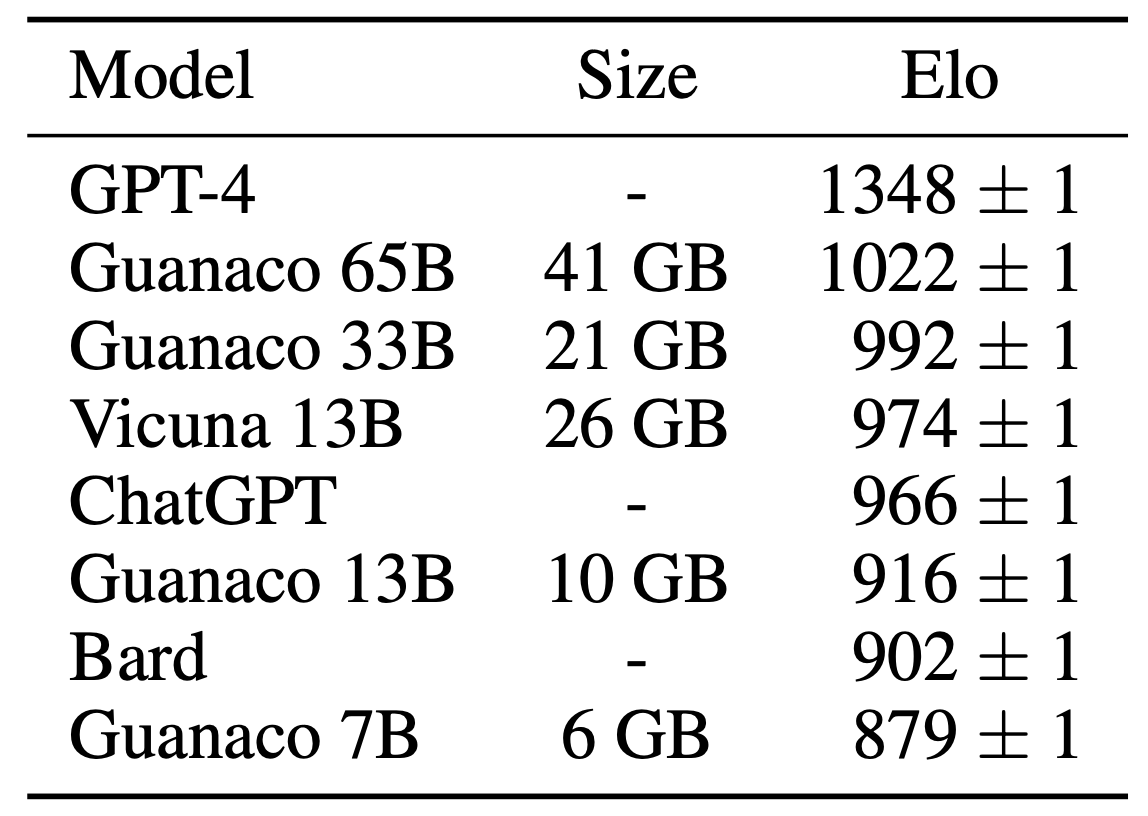
As I described in the previous post, the efficient finetuning method of large language models (LLMs) have been treated as an important work. In this paper, the authors presented QLoRA that acheived quantized 4-bit finetuning without sacrificing model performances. They finetuned publicly available models (such as LLaMA) on a single GPU and named model family as Guanaco. Guanaco 7B to 65B showed comparable or even better performances compared to benchmarks (GPT-4, Vicuna, and Bard) under Elo rating system while using 6GB to 41GB GPU resources.
The authors successfully designed to reduce the cost without any performace degradation through (1) 4-bit NormalFloat, (2) Double Quantization, and (3) Paged Optimizers. Thanks to QLoRA’s efficiency, they also investigated an in-depth study on extensively finetuning over 1,000 models varing on datasets, architectures, and sizes (80M to 65B parameters). In addition, they also analyzed chatbot performance from both human and model-based evaluation (GPT-4).
Methods
4-bit NormalFloat Quantization
The NormalFloat (NF) data type builds on Quantile Quantization [1].
- Quantile Quantization Example (SRAM-Quantiles estimation algorithm)
| Quantization Process | Dequantization Process |
|---|---|
| Optimizer State: -3.1 0.1 -0.03 1.2 Chunk into blocks: (-3.1 0.1) (-0.03 1.2) Find block-wise absmax: 3.1 1.2 Normalize with absmax: (-1.0 0.032) (-0.025 1.0) Find closest 8-bit value: -1.0 0.0329 -0.0242 1.0 Find corresponding index: 0 170 80 255 -> Store index values |
Load index values -> 0 170 80 255 Lookup values: -1.0 0.0329 -0.0242 1.0 Denormalize by absmax: (-1.0 0.0329) * 3.1 (-0.0242 1.0) * 1.2 Dequantized optimizer states: -3.1 0.102 -0.029 1.2 |
Since quantile quantization should estimate the desired quantiles, this process is computationally expensive. Even though SRAM-Qauntiles were proposed to resolve the issue, they still showed large quantization errors for outliers.
Therefore, the authors designed an information-theoretically optimal data type by transforming input tensors to a single fixed normal distribution. Since pretrained neural network weighs a zero-centered normal distribution, they assumed the arbitrary range [-1, 1].
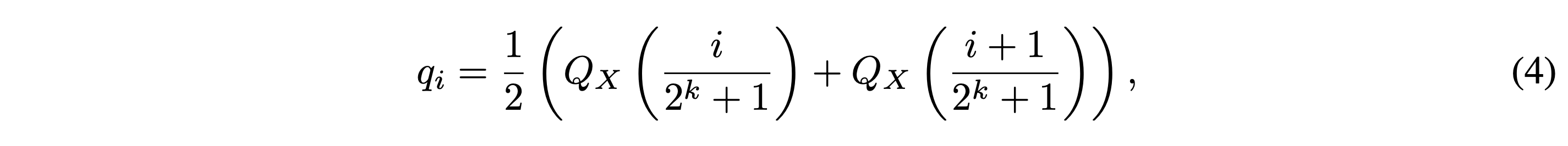

As shown in the equation (4), they first estimate (2^k + 1)~N(0, 1) quantiles, where k is a quantile quantization bit. Then, they normalize its values in to the arbitrary range. Finally, similar to the SRAM-Quantiles estimation algorithm, they used absolute maximum rescaling to quantize the input tensors. Here, Qx() denotes the quantile function of the standard normal distribution N(0, 1), where it represents the inverse of the cumulative distribution function.
They also utilized an asymmetric k-bit quantization by dividing the estimated quantiles qi of two ranges; 2^(k-1) for the negative part and 2^(k-1) + 1 for the positive part. For example, in the case of the asymmetric 4-bit quantization, the quantiles can be estimated into -7 to 0 for the negative part (8 levels) and 0 to 8 (9 levels). Then, the duplicated 0 is removed from one of the two zeros. Through this chain of the process, the authors converted input tensors into NF4 type.
Double Quantization
The authors proposed Double Quantization (DQ) for additional memory savings.
- What is Quantization Constants?
X[Int8] = round(127/absmax(X[FP32])) * X[FP32] = round(c[FP32] * X[FP32])
dequant(c[FP32], X[Int8]) = X[Int8] / c[FP32] = X[FP32], where c is the quantization constant.
Here are the examples of DQ. If we used 32-bit constants and a blocksize of 64 for model weights, quantization constants store 32/64 = 0.5 bits per parameter. On the other hand, DQ treated quantization constants c[FP32] as double quantization steps, i.e., c2[FP8] and c1[FP32]. Therefore, the quantization constants in DQ add 8/64 + 32/(64*256) = 0.127 bits per parameter which reduce 0.373 bits per parameter.
Paged Optimizers
Paged Optimizers handle the GPU out-of-memory issue by leveraging the NVIDIA unified memory solution which performs automatic memory paging between the CPU and GPU. This feature works are similar to regular memory paging between CPU and the disk. Thus, this technique can prevent the GPU memory error while training on the restricted GPU resources. The authors employed this feature to allocate paged memory for the optimizer steps.
QLoRA

The equation (5) represented the QLoRA function. To summarize, QLORA has one storage data type (NF4) and a computation data type (16-bit BrainFloat). They dequantize the storage data type to the computation data type to perform the forward and backward pass, but only compute weight gradients for the LoRA parameters which use 16-bit BrainFloat.
Conclusions
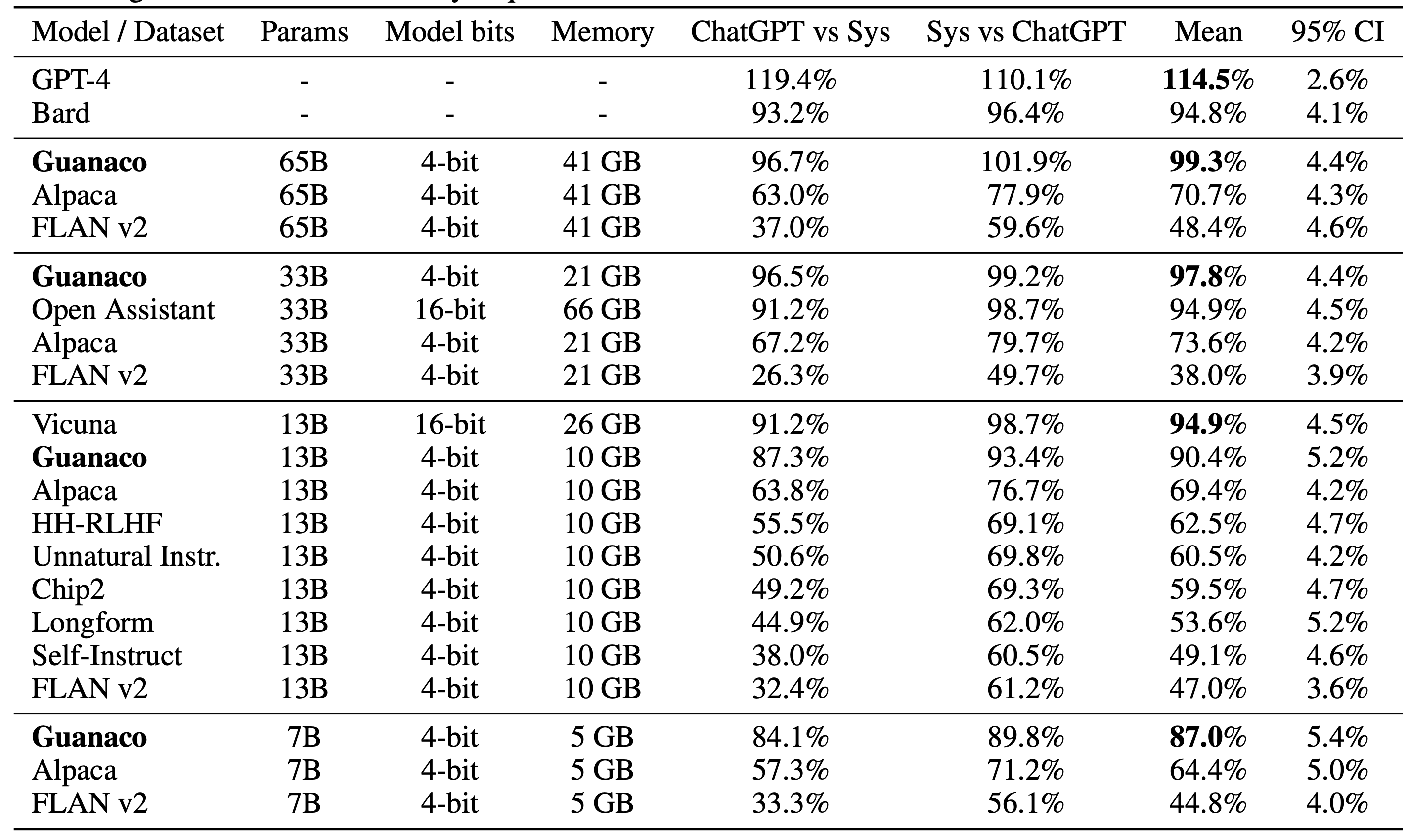
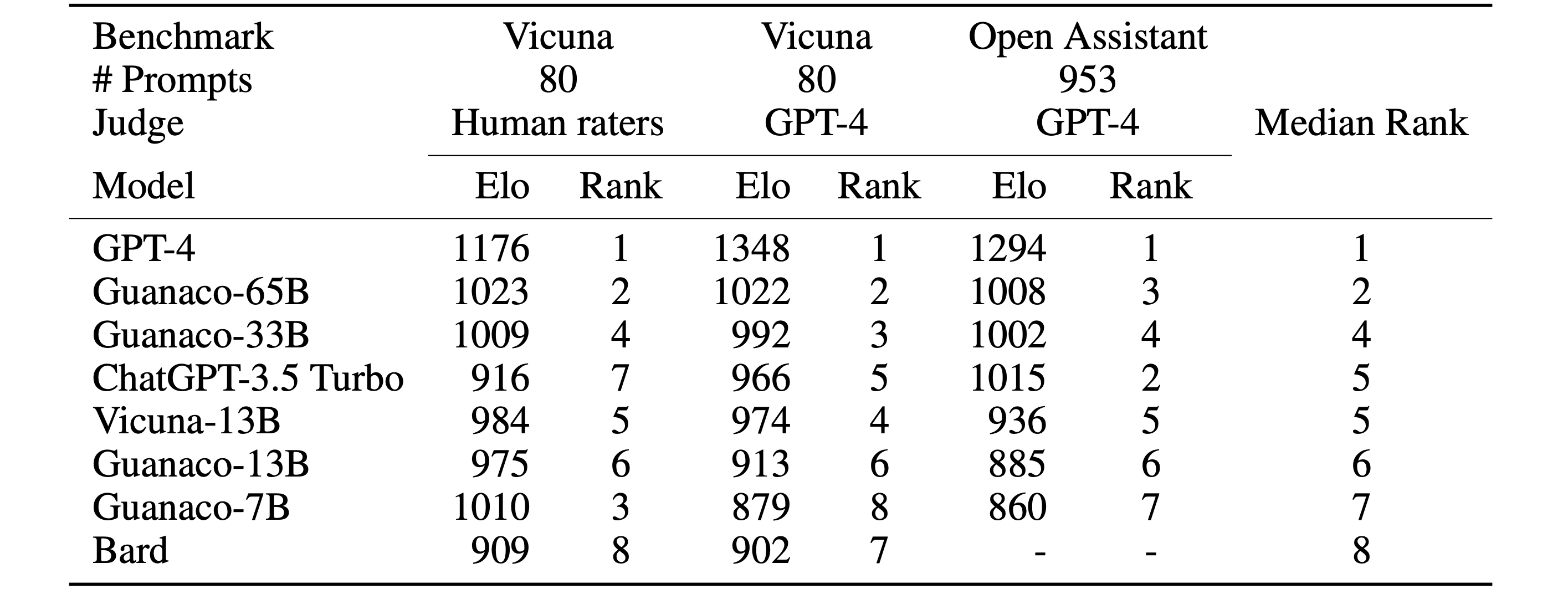
The extensive experimental results demonstrated the effect of QLoRA and QLoRA achieved comparable performance as full-model finetuning. Interestingly, they found that data quality is much more important than the dataset size on chatbot performance according to the quantitative results. They also emphasized the carefulness of choosing between human evaluations and model-based evaluations. Model-based evaluation is a cheap alternative to human annotation, however should take a risk of the assessment quality.
References
[1] Dettmers, Tim, et al. “8-bit optimizers via block-wise quantization.” arXiv preprint arXiv:2110.02861 (2021).
